Phase Locked Loops
There are many excellent references I use for anything connected with phase locked loops (PLLs), in particular Robins (1) and Gardner (2). Much of the information on this page originates from either of these. Synthesisers for a multitude of applications from high stability low phase noise through to fast hopping and beyond are widespread in everyday equipment. Examples of their use are digital cellular communications over the last 30 years or so and, more recently, the move to software defined radio (SDR) in digital transmitters and receivers where they have several uses including sampling frequency sources and local oscillators. Over the same period, synthesizer ICs have progressed from relatively simple dividers, through programmable VCO and reference dividers to the inclusion of phase detectors, loop filters and even VCOs themselves.
A PLL implements a form of negative feedback as used in control theory. This is also used in many other areas of engineering. In the context of an amplifier for example, a feedback circuit is usually designed to feed a portion of voltage from its output to its input, and there are various ways of achieving this. The feedback may be positive (in phase) to design an oscillator or negative (180° out of phase) to perhaps broaden its amplitude frequency response at the expense of reducing gain. It would often be considered in steady state, that is, considering the conditions a long time after any changes have been applied. Where we have to handle potentially fast changes, the best way to analyse it is to use the complex frequency plane: Laplace transforms and their inverses, where necessary.
A PLL works at a fixed frequency and constant phase once a steady lock state has been achieved. A simple example is shown in Figure 1-1 and would typically be used to provide a relatively high level sinusoidal output from a voltage controlled oscillator (VCO), but locked to a high quality, stable, relatively low power 'reference' signal. A VCO provides appreciable signal power, but with relatively crude control of frequency and effectively no control of phase. A reference frequency oscillator, such as a crystal oscillator source, provides a high quality stable frequency source but of limited output power. A well designed PLL provides appreciable sinusoidal power and accurate control over frequency and phase.
The parameter 's' (s=jω) is the complex frequency. Laplace transforms may be used to transform from the time domain to the complex frequency domain. The inverse Laplace transform works in the opposite direction. This is a similar transform to the Fourier transform but it is more appropriate for considering pulses and transients, which are key parameters in PLLs.

The function of the phase detector is to compare the phase of a fed back sample from the VCO, with that of the reference frequency oscillator. The frequency range of the VCO must include that of the reference oscillator and the phase detector. The phase detector output is an error signal proportional to the difference in phase between these two signals, normally just a linearly proportional voltage. The error signal is integrated by the loop filter and used to control the VCO frequency in such a direction that it corrects for the phase error. This is a result of negative feedback. The error signal will reduce to a DC value when phase lock is achieved. Frequency dividers can be used in the feedback and/or reference frequency paths but of course the phase detector input signal frequencies are identical when the PLL is locked.
We always have 3 varying parameters: phase (φ), angular frequency (ω) and time (t) which are related as shown in (1-1).
Whenever phase varies, so does the frequency, since the time is the derivative of phase with respect to angular frequency, (1-2).
(1-3) is (1-2) in integral form.
Although there is a physical electrical connection forming a closed loop, the voltage within that loop is not the only parameter used to control it. Starting at the VCO, a voltage input controls a frequency output or perhaps more precisely, a frequency deviation output relative to a fixed frequency, the natural frequency at which the VCO oscillates. The phase detector provides a voltage output proportional to the difference between the phases of 2 inputs. So we have frequency, phase and voltage. The dimensions of frequency are 1/TIME so we have time as well.
The Second Order Synthesizer Transfer Function
Figure 1-2 is an extension of the phase locked loop but enabling the VCO frequency to be an integer multiple of the phase detector frequency. Transfer functions are shown in terms of complex frequency (s=jω). Different frequencies may be synthesized by changing the frequency division ratio.

In the following list of variables, each one is a function of 's' (s=jω).
- θi(s) is the phase noise voltage of the reference frequency oscillator at the input to the second order PLL.
- θn(s) is the phase noise voltage of the VCO, referenced to its output.
- θ0(s) is the resultant output phase noise voltage from the second order PLL.
- N is the frequency division ratio between the VCO output frequency and the phase detector input frequency.
- F(s) is the transfer function of the loop filter.
- Kf is the phase detector transfer function, or phase detector gain, in V/rad.
- KV is the VCO transfer function or sensitivity in Hz/V.
To start with, ignoring the noise contribution, θn(s) of the VCO, the output of the phase detector is (1-4):

Therefore the output is given by (1-5)

Rearranging these gives the transfer function for the whole circuit, Figure 1-6.

Phase Noise Transfer Function
This equation is the transfer function for the whole closed loop in the complex frequency plane. It describes how the closed loop affects the input noise voltage from the reference oscillator. As we are using functions of complex frequency, all parameters are expressed in voltage amplitude and phase, ignoring for the moment the noise contribution from the VCO, which we will look at later.
It is usually quite safe to assume that N, Kφ and KV are constant with respect to the frequencies within the normally locked range and we can simply substitute the values from the datasheets, taking care where necessary to convert to the correct dimensions. Some datasheets are poorly presented and it might be prudent to actually measure the VCO frequency against the control voltage. F(s), the transfer function of the loop filter itself, is however a function of frequency and we have to digress a little to examine this more closely. We can use a passive or an active loop filter. A passive filter is simpler and more reliable but an active filter can provide more gain and provides more flexibility for adjusting the loop parameters. The operational amplifier used for the active filter will contribute some noise to the loop so a low noise type is recommended.
Passive loop filters are simple and reliable and do not require any voltage rails. Provided the capacitors are high quality low leakage types and the resistor values are as small as possible to minimise the Nyquist/Johnson noise, good performance should be possible. However it may well be difficult to provide enough output voltage to sufficiently drive the control pin of the VCO.
Active filters normally use at least one operational amplifier, and are much more flexible but they need well filtered voltage supplies to minimise the risks of introducing extra conducted noise. Many types of operational amplifiers are available for this type of application including low noise types with good edge performance.
Active Filters
Figure 1-3 shows an active low pass filter in balanced configuration.

Figure 1-4 is an active loop filter, unbalanced configuration.

The voltage transfer function F(s) in Equation 1-7 is defined as the output voltage divided by the input voltage.

Analysing the operational amplifier circuit gives Equation 1-8 :

where

and

The Closed Loop Transfer Function
Substituting the loop filter transfer function F(s) gives, after some manipulation, Equation 1-11

ωn is known as the natural frequency of the loop and is given by Equation 1-12

ωn must not be confused with the cutoff frequency of the low pass filter. However there are some interesting relationships between these which Gardner describes.
ζ is the damping factor, Equation 1-13

Synthesizer Parameters
A frequency synthesizer is piece of equipment which has been designed to synthesize high quality sinusoidal voltage time waveforms to defined parameters, of which the most important are probably frequency and voltage. A synthesizer will typically comprise many internal oscillators and other components, operating at different frequencies and amplitudes, each of which forms part of a phase locked loop. The outputs of these oscillators may be combined in many different ways to generate a versatile range of frequencies and amplitudes at the synthesizer output. In modern synthesizers the operating parameters would normally be programmed from an external input: either directly by the user or by a suitable control interface with a computer or micro-controller.
The performance of a typical synthesizer may be specified using several parameters which are described below.
Phase Noise
Phase noise is perhaps the most important parameter of a synthesizer next to its frequency and amplitude capability. Phase noise originates from random changes in the phase of the continuous wave signal, or carrier, resulting from the operation of the oscillator. Phase noise (Δφ) is synonymous with jitter (Δt) which is the same type of noise but expressed in the time domain for a constant frequency as shown in Equation 1-14.

Equation 1-14 also tells us that, for a fixed level of jitter, the resulting phase noise is directly proportional to the frequency of the carrier. The main sources of phase noise in a PLL are the VCO and the reference frequency source. For a locked loop, the VCO (open loop) phase noise contributes to the overall synthesizer phase noise at large offset frequencies from the carrier and the reference phase noise contributes at small offset frequencies.
By 'offset frequencies' we mean frequencies relative to the nominal carrier frequency. We have to be careful here because some phase noise specifications are at very small offsets, perhaps fractions of a hertz, so we need to have confidence in the frequency accuracy of the carrier.
Figure 1-5 shows an example of a single sideband (SSB) phase noise measurement for a nominal 9.953280 GHz synthesizer, taken from Agilent application note AN 1432. (This frequency is a standard clock frequency for synchronous (optical) telecommunications known at OC-192 (SONET) or STM-64 (SDH)).

This plot is typical of these type of measurements and displays SSB phase noise (density) in dBc/Hz for the oscillator under test across (an offset) frequency range from 1 Hz to 100 MHz. In phase noise plots of this type, it is conventional to describe performance in terms of the offset frequency from the synthesizer nominal frequency which, in this case, is displayed as 9.95328 GHz. We can assume that this oscillator was designed for a sinusoidal output so there should be no or negligible levels of harmonics of the nominal oscillator frequency itself. Sometimes synthesizers are designed to produce square wave waveforms such as TTL, PECL or HTL. The Fourier transform tells us that the spectra of each of these would comprise the fundamental component of the pulse repetition frequency plus harmonics. The phase noise of such devices may be measured, similarly to the sinewave versions but only considering the fundamental component.
The display may be considered to comprise the 'smooth' (random component) part and some discrete components. The random component is mostly phase noise of the type under consideration, but there will be some small contribution from additive white Gaussian noise (AWGN or kTB noise). Near to oscillator frequencies however the phase noise usually dominates. The discrete frequency components are not strictly phase noise but are detected by the phase noise measurement system. The offset frequency scale is logarithmic, which is common with a large frequency range such as this. The vertical scale is also logarithmic as it is expressed in decibels relative to the carrier level, normalised to one hertz bandwidth (dBc/Hz).
The plot displays some interesting characteristics. The general shape of the plot is typical of a phase locked synthesizer. A small rise in the noise level at approximately 2 kHz offset is characteristic of the PLL behaviour where it is necessary to achieve a PLL transfer characteristic damping factor which is neither over or under-damped. This frequency will probably be near the loop filter -3 dB bandwidth. The regions to the left and right are often called 'close to carrier' and 'far from carrier' respectively. For a well designed PLL, the close to carrier and far from carrier noise spectra are dominated by the phase noise contributions from the reference oscillator and the VCO respectively. A degree of noise shaping is sometimes possible in the middle region by adjusting the loop filter characteristics. However this must be performed cautiously because it will also influence the loop characteristics, such as lock time and damping.
Some discrete spurii are apparent between about 50/60 Hz and 900 Hz. These may originate from power supplies (50/60 ) and their harmonics. As power frequency derived spurii like these are difficult to filter and screen, it is common to specify requirements for these separate from the phase noise density itself. There are significant discrete spurii between 1 MHz and 10 MHz. These may originate from other sources in the equipment which are interfering either directly or indirectly with this synthesizer. Some filtering and/or screening development work may be necessary to relax these.
The reference frequency phase noise, also normally open loop, contributes to the synthesizer phase noise primarily in regions close to the carrier. In the synthesizer as a whole, the action of a well designed phase locked loop will actually reduce the phase noise levels in the intermediate offset frequency regions. In general for the synthesizer, the reference oscillator contributes the close to carrier phase noise and the VCO contributes the distant from carrier phase noise. The phase noise profile in between these is a function of the PLL transfer function.
Phase noise is normally expressed as a single sideband (SSB) phase noise power level density (with respect to frequency) either in absolute units or relative to the power of the carrier itself (at zero frequency offset). Typically, this would be displayed on a graph with a vertical axis in units of dBc/Hz across a horizontal axis describing a range of frequency offsets. This represents the measured phase noise power in dB relative to the carrier power normalised to one hertz bandwidth.
Harmonics and Discrete Non-Harmonic Spurii
Harmonics are a subset of discrete spurii. In general, discrete spurii are frequency spectra which occupy a relatively narrow (percentage) bandwidth. Harmonics are discrete spurii located at frequencies that are integer multiples of the desired (fundamental) frequency. Note that, in this case we are taking, not the synthesizer fundamental frequency itself, but the lowest discrete frequency offset. Harmonics and discrete frequencies are specified either as an absolute or a relative unit of power, usually again using logarithmic units such as dBm for absolute power or dBc for relative power. By definition above, discrete spurii are narrow band and it is conventional to consider this close to zero hertz, therefore neither of these is a noise density so units of dBm/Hz or dBc/Hz are not applicable.
These start at the second harmonic which is twice the fundamental frequency, then the third harmonic which is three times the fundamental frequency and so on. Harmonics are of particular interest because they originate only from multiples of the synthesizer fundamental frequency and are not the result of mixing products with any other sources. They are easily generated by any active device, such as an amplifier, if it is not perfectly linear, which is effectively impossible to achieve. No practical amplifier is perfectly linear. In most cases, amplifier non-linearity will generate a range of harmonics and therefore provide potentially many opportunities for further noise problems. In most cases, the levels of harmonics decrease as the order of the harmonic increases and it is not uncommon for the harmonic performance up to the tenth or higher to be specified. Depending on the amplifier architecture, some harmonic multiples will be dominant. For example, a push-pull class B amplifier will generate predominant odd order harmonics.
Non-harmonic discrete spurii potentially have several different sources, for example: spurious oscillations, intermodulation, leakage from other source(s) or various interacting combinations of these. The causes of non-harmonic discrete spurii are usually the most difficult and time-consuming to find as there are usually many potential failure mechanisms which may cause them. To locate and mitigate these requires a methodical and lengthy investigation usually with a well specified spectrum analyzer, probes and other test equipment.
Random Spurii
Random (non-discrete) spurii are apparent as relatively wide areas of noise rising from the noise floor to a broad peak and then tailing off again to the noise floor. These are typically caused by instabilities, levels of positive feedback but not yet sufficient to cause a discrete oscillation. Usually, once the cause of an area of random spurii is found, it may be modified by screening and/or filtering measures to reduce the spurii. Sometimes, it is not possible to solve the random spurious problem, only degrade it. In such cases further investigations may be required.
Noise Floor
The noise floor is taken to be the random noise component visible at the bottom of the phase noise plot at a defined offset frequency. It must be distinguished from any discrete components of the type described earlier, which are a different category. It must be described as a phase noise density: either relative to the carrier power (dBc/Hz) or in absolute units such as dBm/Hz.
Output Power
The output power of a sinusoidal waveform synthesizer is normally interpreted as the long term mean power supplied by the device into a correctly terminated load. In most cases the load is assumed to be exactly 50 Ω and purely resistive. 'Long term' in this context is sometimes referred to as the mean or heating effect power, measured over many cycles. Traditionally, power measurements of this type were precisely that: measurement of the heating effect caused by the applied continuous wave (CW) waveform. Originally, the thermal lag of the heating element, known as a bolometer, may have taken a few seconds to respond after which the equivalent DC heating effect was measured to get the result.
In recent years, sampling and processing technologies and speed have improved so much that real time high resolution measurements of even quite high frequency waveforms is possible. Furthermore, the sampled values may then be processed using a range of mathematically correct algorithms including the root mean square (RMS) relevant to this parameter. The method used is to sample the voltage waveform over sufficient time steps covering one half cycle or a multiple of half cycles. This is chosen because the application of the RMS algorithm squares, as its name implies, the voltage samples, so these would be identical for the positive half-cycle as the negative half-cycle. The RMS voltage VRMS is given by Equation 1-15.

It is important that samples are chosen appropriately according to the arguments discussed. Following on from this the mean (or average) power is then Equation 1-16.
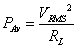
Frequency Accuracy
The frequency accuracy of an oscillator is a measure of how close its actual frequency is to the intended or design frequency, which is often referred to as the nominal frequency. The nominal frequency is the intended frequency, expressed informally, without a detailed specification about accuracy, stability etc.. For example, it is understood that if we refer to 'a 100 MHz oscillator when we mean 'an oscillator with a nominal frequency of 100 MHz'. We have said nothing about any other parameters. Indeed, they might be the subject of a 100 page specification document or datasheet. Do we mean 100.0 MHz, 100.000000 MHz or whatever?
In the phase noise example shown above, a frequency of 9.953280 GHz is indicated. By convention, the number of decimal places used implies the expected accuracy of such a value, in this case to a window of 1 kHz. So the implication here is that there is confidence that the actual frequency is between 9.953279500 GHz and 9.953280500 GHz. However we know nothing about how accurate the frequency display shown on the plot is. Any bit of simple firmware nowadays can generate an impressive looking number to many decimal places but this could be totally meaningless without some traceability to a proper standard, if any, that was used.
To measure a frequency with confidence, it has to be compared in some way against a reference in which we have greater confidence. The rule of thumb is that the reference must have one order of magnitude greater accuracy than the minimum accuracy that is acceptable in the device being tested. Therefore, in the example above, if we could measure the oscillator frequency to a window of 100 Hz instead of 1 kHz, this should be achieved. That would be a 100 Hz window between 9.953278950 GHz and 9.953279050 GHz Even, once this is achieved, it does not guarantee that 100% of all such measurements made in this way will meet the frequency requirement. Nothing is 100% certain, but it will normally be a sufficiently high proportion for most practical purposes, based on a Gaussian (or Normal) distribution.
Frequency Stability
Frequency stability is precisely that: how stable the oscillator frequency is when subject to some external stimulus. The stimulus could be any of several things, most commonly temperature but other examples might be: aging, vibration or supply voltage variation. Needless to say, these other parameters need to be specified, where applicable. Sometimes the frequency stability is actually more important than the frequency accuracy. It depends on the application. If a synthesizer was used as a reference for the frequency used for a radio transmission, accuracy may be the most important parameter. Obviously stability and the other parameters must still be specified but perhaps their requirements may not be as tight.
AM Noise
Amplitude modulated noise or AM noise is sometimes specified in addition to phase noise. As its name implies, it is noise added to the amplitude of the carrier rather than the phase. It is of usually less concern than phase noise because the latter is central to the performance of the phase locked loop and its many performance parameters. One contribution to AM noise is from the amplitude component of thermal or additive white Gaussian noise (AWGN), also known as kTB noise. AWGN comprises random components in both phase and amplitude so its presence would also contribute to phase noise.
Lock Time and Settling Time
Most modern synthesizers have some programming capability. They are designed to operate across a specified range of frequencies and very probably they will be channelised: there will be a minimum frequency step size that they were designed for. To change one of these synthesizers from one frequency to another the internal processor or microcontroller needs to be programmed with the new frequency and other information for feeding the new parameters into the synthesizer IC. These would include the necessary VCO and reference divider ratios and other setup information. There will be a finite time required to program in the new information, to do any necessary processing and then wait for the synthesizer to phase lock at the new frequency. This is generically known as the lock time. However, to be more precise, it normally comprises a frequency re-tune time followed by a phase-lock time added to any processing/programming time. Some synthesizers are designed for frequency agile equipment, where it is required to often and quickly re-tune and lock to new frequencies. In these cases lock time is likely to be a critical requirement.
There is sometimes ambiguity around the definitions of programming, frequency lock, phase lock and settling times. In most cases, it is the sum of all four that is required for agile synthesizers. Specifically, settling time refers to the time for the phase detector output to settle to its final DC value after re-tuning. It therefore relates to the final phase locking process. Normally there would be some type of window threshold requirement either side of zero phase, which is required in a specified time.